Warped Gaussian Process Regression

The bundle of functions for warped Gaussian process regression is contained in the zip folder Test_1d_GPR_public.m

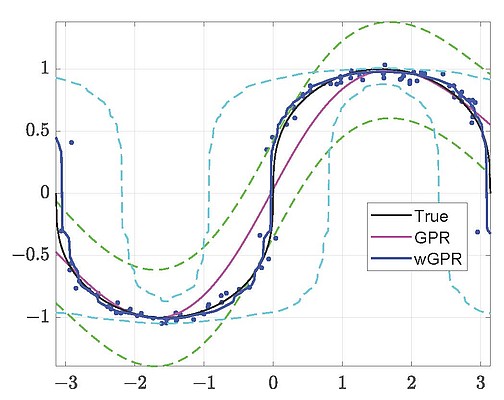
The main file is a script by the same name. The script generates a warped sine function contaminated with noise according to the example in the Snelson et al. 2004 paper. The function is sampled at N points and GPR is performed to estimate the function at Ntest points.  The GPR parameters are estimated by variogram fitting for different variogram models including the Spartan variogram family (see Ref. [3]). 

The GPR equations are solved by means of the covariance kernel-based system (function GPR). The script applies both the GPR and wGPR (warped GPR) algorithms.  Warping is performed using the non-parametric KCDE method presented in Refs. [1], [2] below. The KCDE method is based on the kernel density estimation with the BGK bandwith.

The software has been tested under the following versions: Matlab 2015b and 2023a.

For licensing information see the text files "license_Test1D_GPR_public" and "license_kde" in the zip folder above.

Contact: Dionissios Hristopulos, dchristopoulos<at>tuc.gr

FUNCTIONS USED: Estim_Variogram_Fit, wls_weighted, GPR, cov_ssrf, theor_variograms, 

vario_empir_d,  Gen_Lookup, kcde, KCDF_Estim, KernBW, kernel_i, Kernel_invNS.

The functions: Gen_Lookup, kcde, KCDF_Estim, KernBW, kernel_i, Kernel_invNS

  have been written by Andreas Pavlides.

The function kde.m has been written by Z. Botev and downloaded from Mathworks FIle Exchange.

REFERENCES

When using this software please cite the following:

  1. Agou VD, Pavlides A, Hristopulos DT. Spatial Modeling of Precipitation Based on Data-Driven Warping of Gaussian Processes.  Entropy. 2022; 24(3):321. doi.org/10.3390/e24030321

  2. Andrew Pavlides, Vasiliki D. Agou, Dionissios T. Hristopulos, Non-parametric kernel-based estimation and simulation of precipitation amount, Journal of Hydrology, Volume 612, Part A, 2022, 127988, doi.org/10.1016/j.jhydrol.2022.127988

3. D. T. Hristopulos, Random Fields for Spatial Data Modeling: A Primer for Scientists and Engineers. Springer Netherlands, Dordrecht, 2020, ISBN  978-94-024-1918-4, doi: 10.1007/978-94-024-1918-414,  URL: doi.org/10.1007/978-94-024-1918-4_14.

For the KDE method with BGK bandwidth cite the paper:

Botev, Z.I., Grotowski, J.F., Kroese, D., 2010. Kernel density estimation via diffusion. Ann. Stat. 38 (5), 2916–2957.