New probability distributions with modified tail behavior

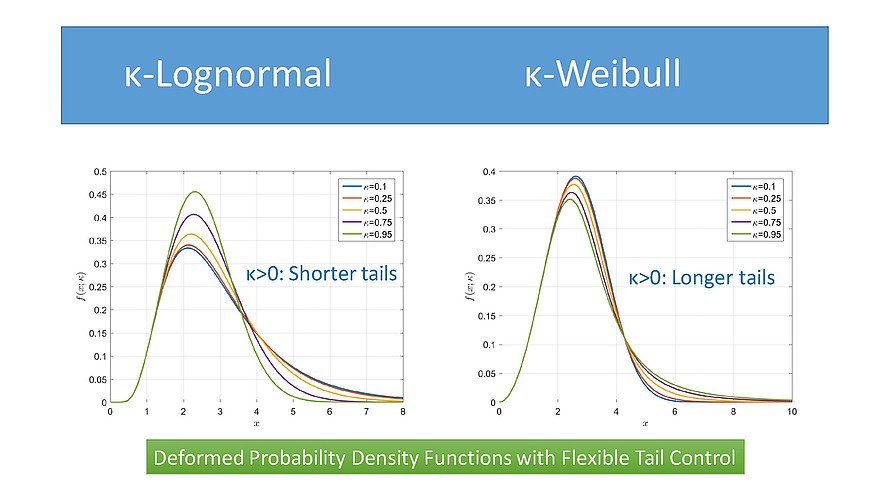
Probabilistic models with flexible tail behavior have important applications in engineering and earth science. We introduce a nonlinear normalizing transformation and its inverse based on the deformed lognormal and exponential functions proposed by Kaniadakis. The deformed exponential transform can be used to generate skewed data from normal variates. We apply this transform to a censored autoregressive model for the generation of precipitation time series. We also highlight the connection between the heavy-tailed κ-Weibull distribution and weakest-link scaling theory, which makes the κ-Weibull suitable for modeling the mechanical strength distribution of materials. Finally, we introduce the κ-lognormal probability distribution and calculate the generalized (power) mean of κ-lognormal variables. The κ-lognormal distribution is a suitable candidate for the permeability of random porous media. In summary, the κ-deformations allow for the modification of tails of classical distribution models (e.g., Weibull, lognormal), thus enabling new directions of research in the analysis of spatiotemporal data with skewed distributions.