Gaussian Anamorphosis with Kernel Function Estimators for Spatially Distributed Data and Time Series with Applications in Precipitation Analysis

Using Kernel Functions to Estimate the Probability Distribution of Skewed Data
The probability distribution of precipitation amount strongly depends on geography, climate zone, and time scale considered. Closed-form parametric probability distributions are not sufficiently flexible to provide accurate and universal models for precipitation amount over different time scales. In this paper we derive non-parametric estimates of the cumulative distribution function (CDF) of precipitation amount for wet time intervals. The CDF estimates are obtained by integrating the kernel density estimator leading to semi-explicit CDF expressions for different kernel functions. We investigate kernel-based CDF estimation with an adaptive plug-in bandwidth (KCDE), using both synthetic data sets and reanalysis precipitation data from the island of Crete (Greece). We show that KCDE provides better estimates of the probability distribution than the standard empirical (staircase) estimate and kernel-based estimates that use the normal reference bandwidth. We also demonstrate that KCDE enables the simulation of non-parametric precipitation amount distributions by means of the inverse transform sampling method.
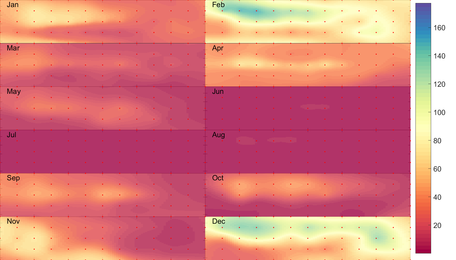
Space-Time Analysis of Precipitation Reanalysis Data for the Island of Crete using Gaussian Anamorphosis with Hermite Polynomials
- Climate change poses a serious threat to environmental and economic sustainability
- Lack of a universal probability distribution that can fit monthly precipitation data
- Spatial variability of rainfall and dependence on complex topography
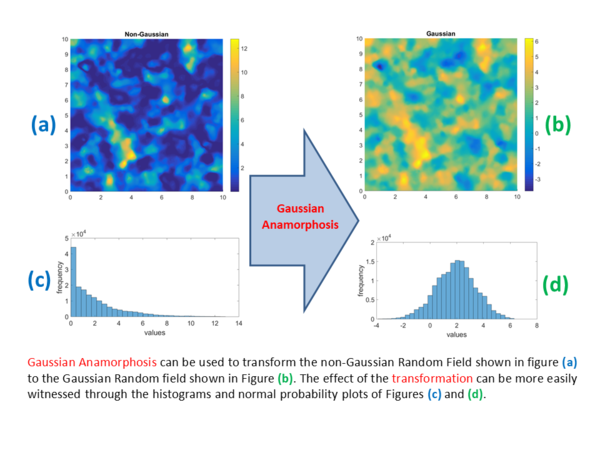
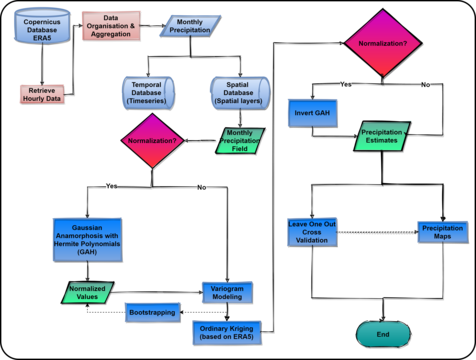
- We investigate flexible normalizing transformations for the geostatistical analysis of precipitation
- We generate new, improved precipitation maps and uncertainty estimates based on reanalysis data for the island of Crete
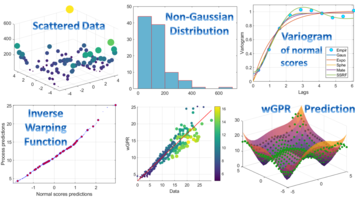
Cross-validation shows improved performance of Gaussian anamorphosis with Hermite polynomials
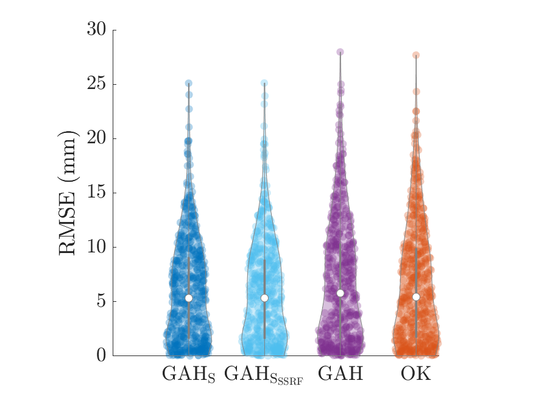
Using cross-validation it was shown that the maps obtained using Gaussian anamorphosis with Hermite polynomials are more accurate than those generated by means of the standard Ordinary Kriging approach.